PCA
import numpy as np
import sklearn
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.datasets import fashion_mnist
import seaborn as sns
import os
import gzip
import sys
# The number of components for pca
N_COMP = 100 #@param {type:"integer"}
#Load data:
(X_train, y_train), (X_test, y_test) = fashion_mnist.load_data()
#Design matrix
print('Design matrix size: {}'.format(X_train.shape))
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz
32768/29515 [=================================] - 0s 0us/step
40960/29515 [=========================================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz
26427392/26421880 [==============================] - 0s 0us/step
26435584/26421880 [==============================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz
16384/5148 [===============================================================================================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz
4423680/4422102 [==============================] - 0s 0us/step
4431872/4422102 [==============================] - 0s 0us/step
Design matrix size: (60000, 28, 28)
# select only 10000 entries
X = X_train[:10000].reshape(10000, 28*28)
y = y_train[:10000]
print('Design matrix size: {}'.format(X.shape))
Design matrix size: (10000, 784)
# Each class is equally distributed
plt.hist(y, bins=10)
(array([ 942., 1027., 1016., 1019., 974., 989., 1021., 1022., 990.,
1000.]),
array([0. , 0.9, 1.8, 2.7, 3.6, 4.5, 5.4, 6.3, 7.2, 8.1, 9. ]),
<BarContainer object of 10 artists>)

#@title
scaler = MinMaxScaler() #@param ["StandardScaler()", "MinMaxScaler()"] {type:"raw"}
#Normalize features:
X_norm = scaler.fit_transform(X)
#Apply PCA:
pca = PCA(n_components=N_COMP)
X_norm_r = pca.fit(X_norm).transform(X_norm)
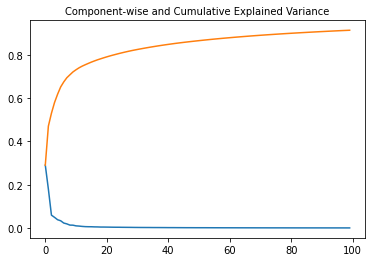
#Plot Component-wise and Cumulative Explained Variance:
plt.subplot(1, 1, 1)
plt.plot(range(N_COMP), pca.explained_variance_ratio_)
plt.plot(range(N_COMP), np.cumsum(pca.explained_variance_ratio_))
plt.title("Component-wise and Cumulative Explained Variance", fontsize=10)
Text(0.5, 1.0, 'Component-wise and Cumulative Explained Variance')
SAMPLE_INDEX = 1 #@param {type:"integer"}
#Invert the PCA to obtain the image with the new components:
inv = pca.inverse_transform(X_norm_r[SAMPLE_INDEX, :])
inv = scaler.inverse_transform(inv.reshape(1, -1)) #Unnormalize
# first and second component shows 19.90816038%, 12.3440578% variance
pca.explained_variance_
array([19.90816038, 12.3440578 , 4.08476887, 3.38992731, 2.63359359,
2.30695522, 1.58484872, 1.32275233, 0.93530702, 0.90874507,
0.69233472, 0.62360634, 0.51991806, 0.44841116, 0.4206539 ,
0.4118544 , 0.37067912, 0.35583739, 0.31561593, 0.31384498,
0.29923304, 0.28435846, 0.26687049, 0.25671446, 0.2542121 ,
0.23751597, 0.22886912, 0.22020005, 0.21188035, 0.19669937,
0.1894092 , 0.1812197 , 0.17766722, 0.17156967, 0.16977035,
0.16029575, 0.15733769, 0.15434082, 0.14819601, 0.14438449,
0.13662726, 0.13589267, 0.13338509, 0.12585236, 0.12322937,
0.1178111 , 0.11334105, 0.11301685, 0.11036387, 0.10593086,
0.10428265, 0.10398582, 0.10232937, 0.09886198, 0.09775931,
0.0937765 , 0.0925225 , 0.08998517, 0.08742279, 0.08642101,
0.08522065, 0.08342365, 0.0820813 , 0.07886205, 0.07877769,
0.07697806, 0.07613849, 0.07481195, 0.07302077, 0.07074866,
0.06983124, 0.0690006 , 0.06799822, 0.06494334, 0.06449241,
0.06382796, 0.06350159, 0.06318037, 0.06059633, 0.05935327,
0.05789755, 0.05752058, 0.05716922, 0.05522969, 0.05458889,
0.05392811, 0.05366838, 0.05260112, 0.05206034, 0.05165089,
0.05045936, 0.04969883, 0.04947893, 0.04776872, 0.0474947 ,
0.04667546, 0.04579855, 0.04476067, 0.04342998, 0.04284381])
# Compute PCA to get the last components (in order of decreasing variance):
# Not sure how to do this in sklearn
X_norm = X_norm.T #Transpose the design matrix to match the formulas
S = X_norm @ X_norm.T #Covariance matrix
eigvals, eigvecs = np.linalg.eig(S) # compute eigenvalues and eigenvectors
order = np.argsort(eigvals) #sort eigenvalues in ascending order (add [::-1] to get descenging order)
B = eigvecs[:, order[:N_COMP]] #Take the last N_COMP eigenvectors as new basis
C = B.T @ X_norm #Code: projection of X in the subspace spanned by the columns of B
X_rec = B @ C #revert the tranformation to project the code back in the original space
X_rec = X_rec.T #Bring back the dimensions to the original convention
X_rec = scaler.inverse_transform(X_rec) #Unnormalize
#Plot images:
fig, axarr = plt.subplots(1, 3, figsize=(12, 4))
sns.heatmap(X[SAMPLE_INDEX, :].reshape(28, 28), cmap='gray_r', ax=axarr[0])
sns.heatmap(inv.reshape(28, 28), cmap='gray_r', ax=axarr[1])
sns.heatmap(X_rec[SAMPLE_INDEX, :].reshape(28, 28), cmap='gray_r', ax=axarr[2])
axarr[0].set_title("Original image\n({} components)".format(X.shape[1]), fontsize=12)
axarr[1].set_title("First {} components image".format(N_COMP), fontsize=12)
axarr[2].set_title("Last {} components image".format(N_COMP), fontsize=12)
axarr[0].set_aspect('equal')
axarr[1].set_aspect('equal')
axarr[2].set_aspect('equal')
axarr[0].axis('off')
axarr[1].axis('off')
axarr[2].axis('off')
plt.show()

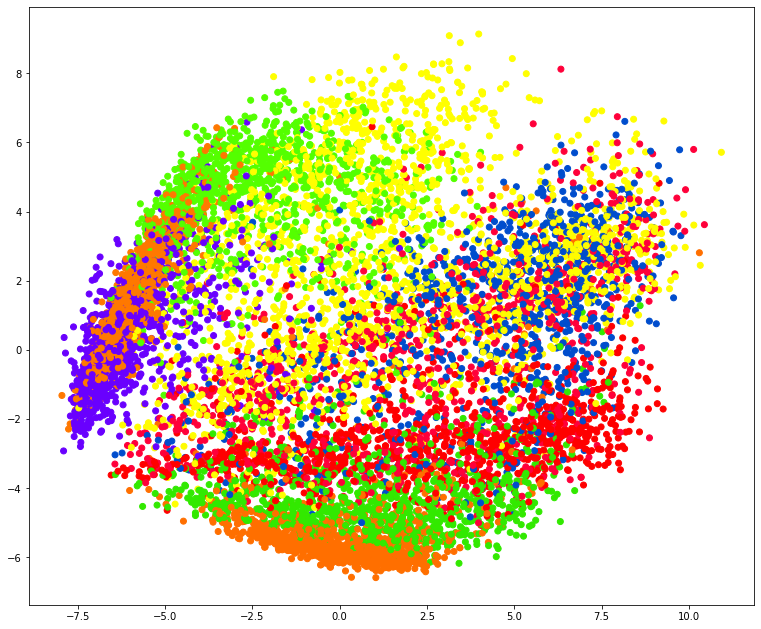
plt.figure(figsize=[13, 11])
plt.scatter(X_norm_r[:, 0], X_norm_r[:, 1], c=y, cmap='prism')
plt.savefig('pca_scatter.png', dpi=200, bbox_inches='tight')
Autoencoder
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
import math
from sklearn.metrics import accuracy_score, precision_score, recall_score
from sklearn.model_selection import train_test_split
from tensorflow.keras import layers, losses
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Model
from tensorflow import keras
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
How simple is MNIST!!
We are able to compress 28x28=786 size image into 3x3=9 image
encoder_size = 196 #@param ["196", "64", "9"] {type:"raw"}
Creating an AutoEncoder
# encoder_input = keras.Input(shape=(28,28,1), name="img")
# x = keras.layers.Flatten()(encoder_input)
# encoder_output = keras.layers.Dense(encoder_size, activation="relu")(x)
# encoder = keras.Model(encoder_input, encoder_output, name="encoder")
# decoder_input = keras.layers.Dense(784, activation="relu")(encoder_output)
# decoder_output = keras.layers.Reshape((28, 28, 1))(decoder_input)
# opt = keras.optimizers.Adam(lr=0.001, decay = 1e-6)
# autoencoder = keras.Model(encoder_input, decoder_output, name="autoencoder")
# autoencoder.summary()
Creating a Linear AutoEncoder with hidden size 2
i.e. We are compressing a 28x28 image in 2x1 pixel
encoder_input = keras.Input(shape=(28,28,1), name="img")
x = keras.layers.Flatten()(encoder_input)
encoder_output = keras.layers.Dense(2, activation="linear")(x)
encoder = keras.Model(encoder_input, encoder_output, name="encoder")
decoder_input = keras.layers.Dense(784, activation="linear")(encoder_output)
decoder_output = keras.layers.Reshape((28, 28, 1))(decoder_input)
opt = keras.optimizers.Adam(lr=0.001, decay = 1e-6)
autoencoder = keras.Model(encoder_input, decoder_output, name="autoencoder")
autoencoder.summary()
Model: "autoencoder"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
img (InputLayer) [(None, 28, 28, 1)] 0
_________________________________________________________________
flatten (Flatten) (None, 784) 0
_________________________________________________________________
dense (Dense) (None, 2) 1570
_________________________________________________________________
dense_1 (Dense) (None, 784) 2352
_________________________________________________________________
reshape (Reshape) (None, 28, 28, 1) 0
=================================================================
Total params: 3,922
Trainable params: 3,922
Non-trainable params: 0
_________________________________________________________________
/home/bread/.local/lib/python3.9/site-packages/keras/optimizer_v2/optimizer_v2.py:355: UserWarning: The `lr` argument is deprecated, use `learning_rate` instead.
warnings.warn(
autoencoder.compile(opt, loss="mse")
X.shape
(10000, 784)
# The shape of X is (10000, 784) but our network needs (something. 28, 28) form
autoencoder.fit(X.reshape(-1, 28, 28), X.reshape(-1, 28, 28), epochs=3, batch_size=32)
Epoch 1/3
313/313 [==============================] - 0s 936us/step - loss: 5566.6777
Epoch 2/3
313/313 [==============================] - 0s 932us/step - loss: 3276.6267
Epoch 3/3
313/313 [==============================] - 0s 863us/step - loss: 3193.3284
<keras.callbacks.History at 0x7fcf23f10d30>
example = encoder.predict([X_test[0].reshape(-1, 28, 28, 1)])[0]
example
array([ -8.0858965, 1192.9724 ], dtype=float32)
example.shape
(2,)
# plt.imshow(example.reshape(int(math.sqrt(encoder_size)), int(math.sqrt(encoder_size))), cmap="gray")
plt.imshow(example.reshape(2, 1), cmap="gray")
<matplotlib.image.AxesImage at 0x7fcf18422d00>

Orignal test image
plt.imshow(X_test[0], cmap="gray")
<matplotlib.image.AxesImage at 0x7fcf18381c10>

Encoded test image
ae_out = autoencoder.predict([X_test[0].reshape(-1, 28, 28, 1)])[0]
plt.imshow(ae_out.reshape(28,28), cmap="gray")
<matplotlib.image.AxesImage at 0x7fcf1830fd90>

posttrain_encodings = encoder(X_test).numpy()
posttrain_encodings.shape
(10000, 2)
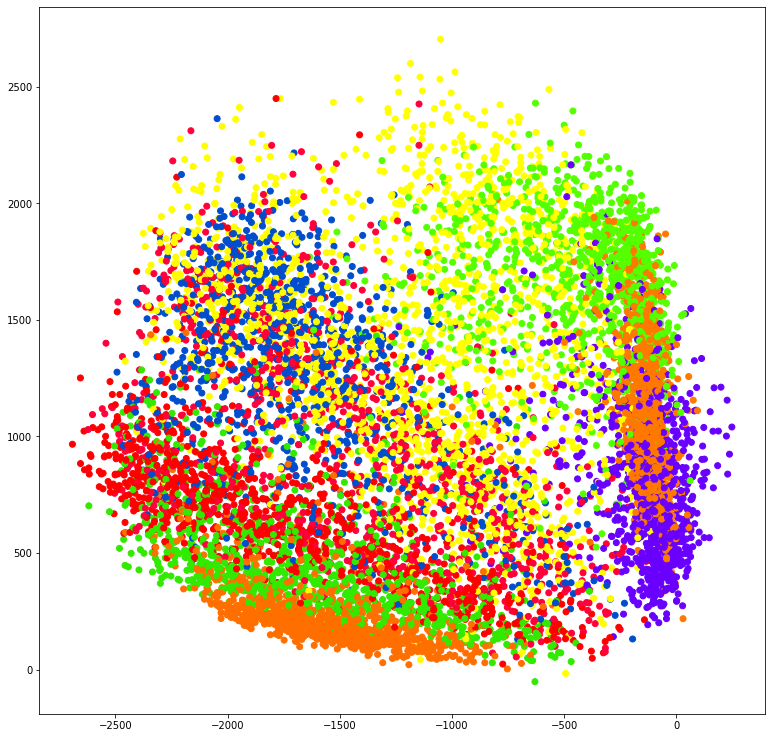
plt.figure(figsize=[13, 13])
plt.scatter(posttrain_encodings[:, 0],
posttrain_encodings[:, 1], c=y_test, cmap="prism")
plt.savefig('linearautoencoder_scatter.png', dpi=200, bbox_inches='tight')
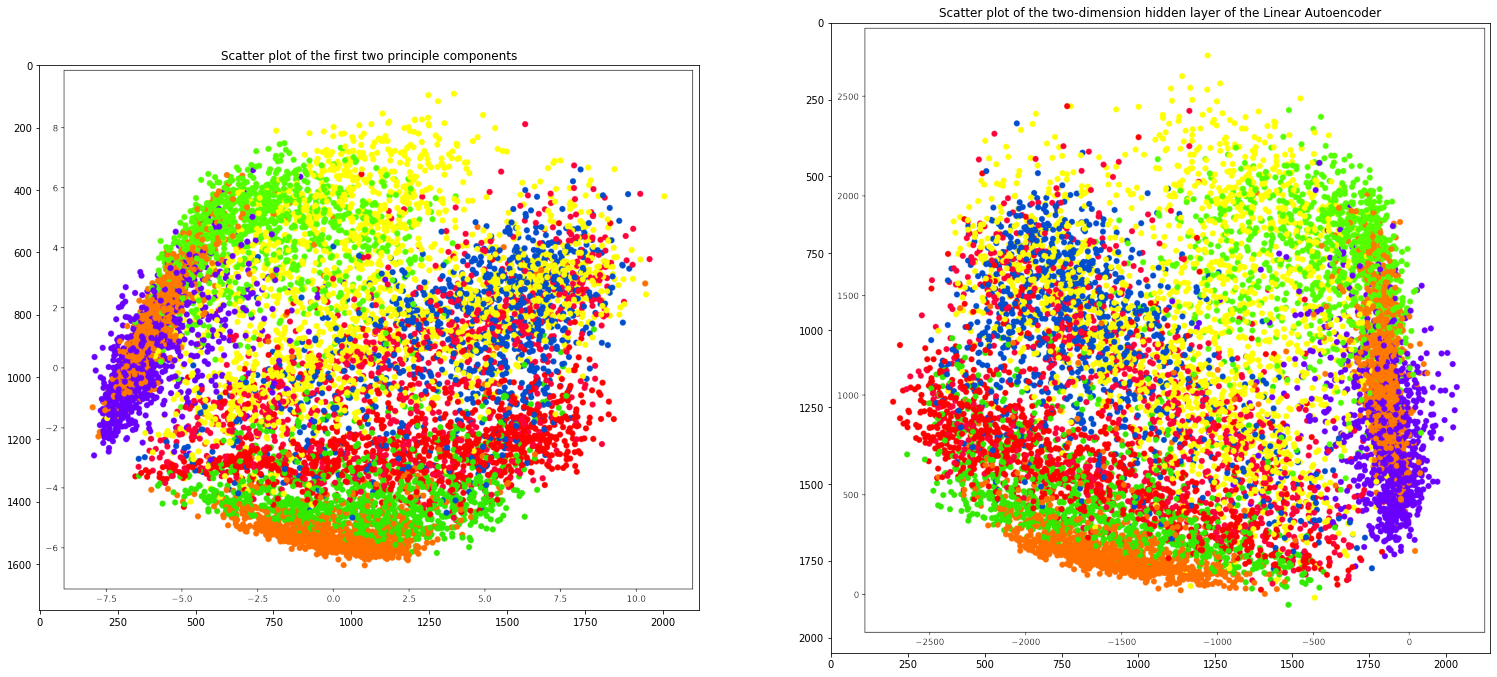
Comparing both the plots
import matplotlib.image as mpimg
plt.figure(figsize=(26, 12))
plt.axis('off')
plt.subplot(1, 2, 1)
plt.title('Scatter plot of the first two principle components')
plt.imshow(mpimg.imread('pca_scatter.png'))
plt.subplot(1, 2, 2)
plt.title('Scatter plot of the two-dimension hidden layer of the Linear Autoencoder')
plt.imshow(mpimg.imread('linearautoencoder_scatter.png'))
<matplotlib.image.AxesImage at 0x7fcf18395a90>